Fleiss’s Kappa - The Key to Validating Data Labeling in Machine Learning

The Problem to Solve

Part of the power of Machine Learning relies on how data is labeled. It is crucial that, beforehand, an expert labels the information used to train ML models.
For example, a doctor might classify whether a patient is healthy or sick.

The Problem With Expert Labeling - Manual Labeling

[!cue] Variety in Diagnosis (Confidence in Result)

Due to the natural variability in human expert labeling, especially across different diagnoses, discrepancies between scorers can occur.
If we want to assess the confidence in how the data is labeled, we need to apply metrics designed for inter-rater reliability such as Fleiss’ Kappa.

[!NOTE] These metrics help quantify the level of agreement beyond chance, ensuring that the labeled data used to train Machine Learning models is both consistent and trustworthy.

How Does Kappa Fix that Problem?

[!cue] Consensus of Agreement

By measuring the degree of agreement, (consensus in the results) between scorers (expert decisions in the labeled data):

• The metric typically ranges from 0 to 1, but can also take on negative values when agreement is worse than chance.
• A value closer to 1 indicates a higher degree of agreement among scorers.

Calculation of Agreement by Expected Chance

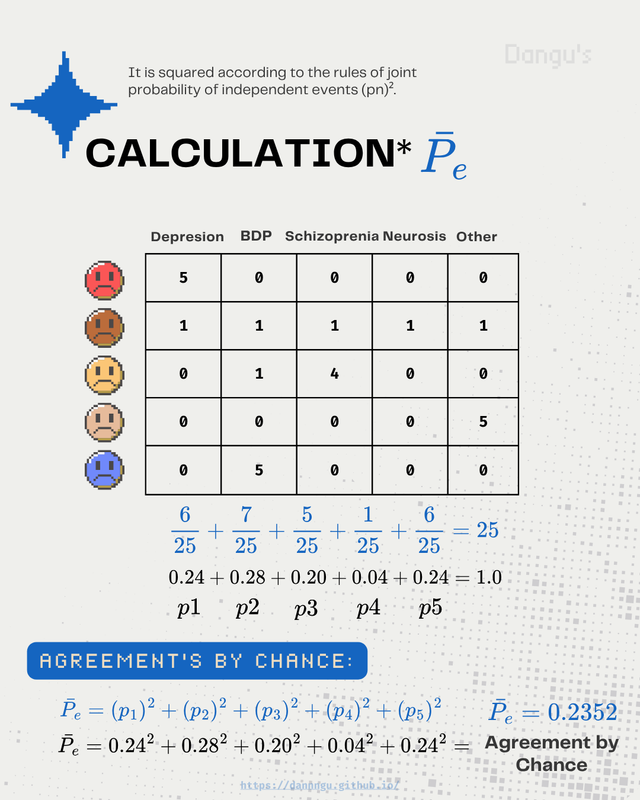
1. First: We sum all the agreements made by the scorers for each column. This gives us the total score per option.
2. Second: We divide each column’s score by the total number of agreement points (25). This normalizes the values into probabilities.
3. Third: We now have the probability of selecting each option if the choice were made randomly like drawing a ball from a bag. The sum of all these probabilities equals 1.
4. Fourth: We square each probability. This follows the rule for combining independent events specifically, the joint probability when both events are the same.

Calculation of Observed Agreement

1. First: Observed Agreement is calculated by summing the actual agreements between the raters. That is, how many times they agreed on the same category.
2. Second: To avoid inflating the result due to trivial agreements (such as a rater repeating themselves), the probability of a match for the same scorer is excluded. This is done by subtracting that portion or adjusting the count so that only matches between different raters are considered.
3. Second: We normalize the data by the total amount of scorers punctuation ($20/20$).
4. Third: We get ($3.6$), so now divide that by the number of scorers ($5$). The result ($3.6/5=0.72$).

   Result & Interpretation

1. First: we use the kappa formula to get the result, in this case $0.63389$
2. Second: we use the table to determinate if the score is good.

• Previous
  N-Grams - NLP in Python